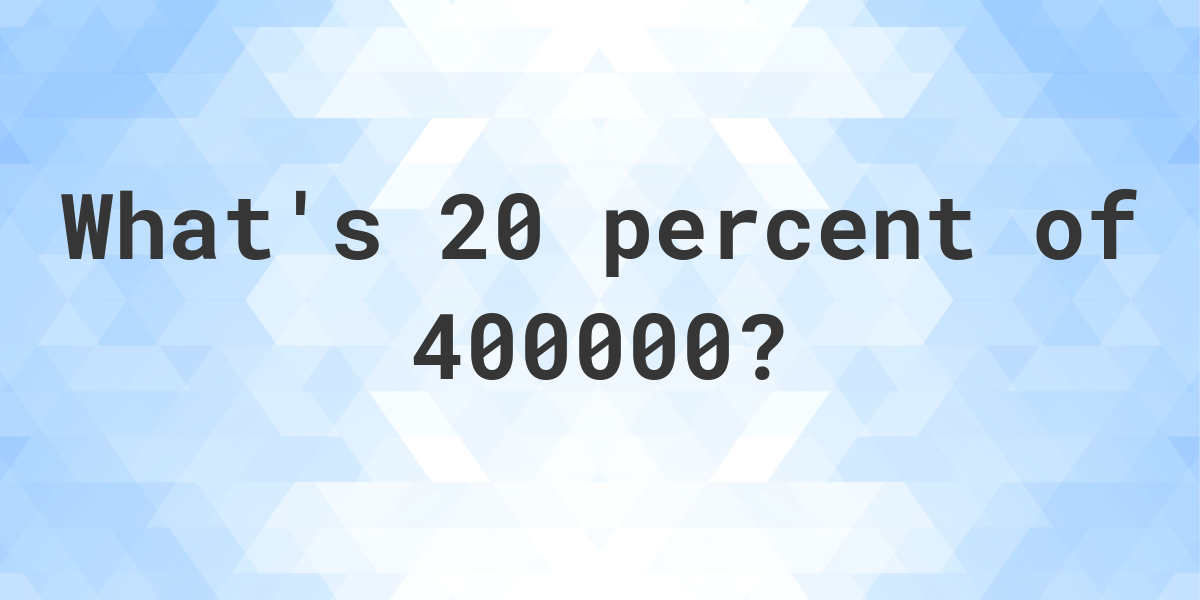Understanding percentages is a fundamental skill in many domains, from mathematics to finance and beyond. One common calculation people encounter is determining what a specific percentage of a number is. This article elucidates the calculation of 20 percent of 400,000, illuminating various aspects related to this numerical query.
The first step in addressing the question “What is 20 percent of 400,000?” is to comprehend the concept of percentages. A percentage represents a fraction out of 100, making it easier to quantify parts of a whole. In this case, you want to calculate a fifth (20/100) of the number 400,000. The mathematical formulation for this operation is straightforward: multiply the number by the percentage expressed as a decimal.
To execute this calculation: convert 20 percent to a decimal. This transition involves dividing 20 by 100, yielding 0.20. The next step is to multiply this decimal by 400,000:
0.20 * 400,000 = 80,000
Thus, 20 percent of 400,000 equals 80,000. This result can be contextualized further by drawing connections to real-world applications. Knowing how to calculate percentages can significantly aid in comprehending financial decisions, budgeting, or even assessing performance metrics in various fields, such as sales and marketing.
In a fiscal context, for instance, businesses frequently use percentage calculations to identify profit margins, commission rates, and discount offers. If a company projects earning 400,000 dollars in revenue, recognizing that they might allocate 20 percent of that sum for marketing or operational expenses could prove instrumental for budgetary planning. This allocation amounts to 80,000 dollars, providing clarity around resource distribution.
Moreover, the utility of calculating percentages extends into the realm of investment. Imagine an investment portfolio that equates to 400,000 dollars; if an investor desires to channel 20 percent of their overall investment into a particular asset, they would choose to invest 80,000 dollars. This strategic decision showcases the practicality of understanding percentages in managing finances effectively.
Besides financial applications, calculating percentages plays an essential role in educational contexts. Teachers often employ percentage-based assessments to determine student performance. A student might score 400,000 points in an annual academic competition. If achievements are assessed by awarding 20 percent of that score for participation, students would essentially recognize the value of engaging in the process, with 80,000 points reflecting their effort.
Furthermore, the concept of percentiles in statistics brings forth another layer of understanding. When discussing data sets, marking the top 20 percent could reveal insights about traits, behaviors, or performance levels among a population. If the total population reflects a numeric benchmark of 400,000, analyzing the upper echelon—those scoring 80,000 or above—could illuminate exceptional performance or anomalies pertinent to the study.
Graphs and visual aids augment comprehension, especially when dealing with sizeable numbers. A graphical representation demonstrating 400,000 with a highlighted section illustrating the 80,000 could provide visual clarity on the relationship between parts and the whole. Such visual tools can simplify complex information, making it accessible for varied audiences.
Delving deeper into the gravity of percentages, distinguishing between simple and compound percentage applications is vital. For instance, while the primary calculation addressed simple percentage computation, scenarios involving compound percentages yield different results. If one were to consider a financial return with 20 percent compounded annually on 400,000, the calculations would cascade over numerous periods, yielding significantly more than 80,000, depending on the duration of the investment.
Moreover, understanding the failure to grasp percentages could lead to critical misjudgments. Misinterpretation in professional settings could result in allocating too little or too much in budgetary matters. Miscalculating performance metrics could jeopardize project evaluations, demonstrating the necessity of accuracy in these calculations.
To reinforce this concept and its diverse applications, educational resources have emerged to provide tools for learners. Interactive calculators and applications now allow individuals to quickly assess any percentage of numbers, solidifying understanding through practice. Workshops focusing on financial literacy often utilize such exercises, thereby equipping participants with better financial acumen.
In conclusion, the determination of what constitutes 20 percent of 400,000 transcends mere numerical computation. It encapsulates a wide array of practical applications across finance, education, and statistics. Calculating 80,000 serves as an illustrative example, guiding individuals in confronting budgets, investments, and assessments with greater confidence and clarity. As we understand the implications of such calculations, we uncover not only the arithmetic behind percentages but also the profound impact they hold in both daily life and broader hypothesized scenarios.